Mathematicians proved the hypothesis on which scientists fought for more than 40 years

2017-12-18 09:27

Mathematicians proved the hypothesis on which scientists fought for more than 40 years
A proven hypothesis about the coverage of areas formulated by the Hungarian mathematician Laszlo Fejes One in 1973.

Sign up for news “UkrMedia” in Facebook, Twitter or Google+

Scientists Alexander Polyanskiy (MIPT, Russia) and Jilin Jiang (Technion, Israel) proved the hypothesis of the coverage of areas formulated by the Hungarian mathematician Laszlo Fejes He was still in 1973: “If several zones covers the unit sphere, their total width at least PI”. The result is important for the development of discrete geometry and gives the possibility of setting new targets. The proof was published in the journal Geometric and Functional Analysis.

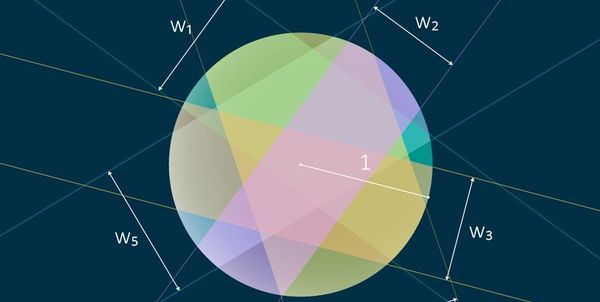
The problem solved by Tarski: full coverage of a circle of unit radius into strips so that their total width not less than 2 (the diameter of the circle). Each of the five bands has its own width and labelled with a unique color.

Discrete geometry studies the combinatorial properties of points, lines, circles, polygons and other geometric objects. For example, it allows to answer the question: what is the smallest number of balls of the same size can be placed around one of the same bowl as the most densely tile the plane with circles of the same space or the same bullets, etc. the Results of some of these tasks are now being applied in practice: for example, the problem of dense packing allows to optimize encoding and error correction in the transmission of information. The proof of the theorem of the four colors, which confirms that all are located on the field map can be colored in no more than four distinct colors so that neighboring countries were not the same color, has prompted mathematicians to develop relevant concepts of graph theory, without which it is impossible to imagine today, many developments in chemistry, biology, computer science, any of the logistics system and so on?D.

Yellow color on the surface of a sphere indicated one area of the width ?

Hypothesis Laszlo Toth Faes closely related to other problems in discrete geometry about covering bands resolved in the twentieth century. Initially, the task was to cover a circle with the strips enclosed between parallel lines, more commonly known as the problem on the boards. Mathematician Tarski gracefully and just proved that the total width of these strips-planks does not exceed the diameter of the circle, regardless of their number: that is better than one plate, the width of which is the diameter of the circle, to cover not. Bang solved the problem of coating strips of arbitrary convex body, namely, it was proved that if a few strips covering a convex body, their total width at least the width of the body, etc?that is, the minimum width of one strip, covering the body.

Full coverage of areas. Each of the five zones has a width and labelled with a unique color

The objective, which worked for the authors, is fundamentally different from previous: it is necessary to examine the coating of the sphere with unit radius with specially constructed areas. Namely, each zone corresponds to a specific three-dimensional strip-plank (just the fact that lies between two parallel planes which are symmetrical relative to the center of the sphere) and is its intersection with the sphere. You can enter another definition, not associating the zone with the strips: the width area ? on the surface of a sphere with unit radius is called the set of points located at a distance of no more than ?/2 from the great circle (the equator) in the geodesic metric (t?that is, the distance between two points is equal to the length of the smallest arc connecting them). Mathematicians needed to find the minimum total width of several such zones, covering the unit sphere. The main difference from the previous measurement width: the normal width of the strips is the Euclidean distance between the parallel lines or parallel planes, and this case is the length of the arc.

In the proof the authors were inspired by the idea of Banga, which is used to solve the problem of covering of the body strips the design of a special nite set of points inside the body, one of which is not covered by the strips. Mathematics, like Bang, was in a sense the contrary: it was assumed that the sum of the widths of the zones completely cover the sphere, less ?, and wanted to get a contradiction: find a point that lies on the sphere, but not covered by zones.

Hypothesis Faes Laszlo Toth. Cover of the sphere with unit radius zones of equal width. The minimum total width of the zones equal ?. Each zone is designated a unique color.

The authors showed that it is possible to build such a set of points in three-dimensional space to at least one point was not covered by strips forming zone. If all these points will be inside the sphere, it will be easy to build a point on it, not covered by the strips, and hence areas. If some of the points will be outside of the sphere, in this case it is possible to replace the multiple zones as one big zone with a width equal to the sum of all widths of these zones. Thus, it is possible in the original problem to reduce the number of zones, but not change their total width, that is, at some point will be able to find a point on the sphere not covered by the zones. This contradicts the fact that the sum of the widths of the zones less ?, it proves the hypothesis Faes Laszlo Toth.

The problem was solved in n-dimensional space, but, according to scientists, this statement and proof does not differ from the three-dimensional case.

Alexander Polyanskiy, of the Department of discrete mathematics, MIPT, one of the authors of “Laszlo Thoth Fees attracted the attention of mathematicians working in discrete geometry for more than 40 years. In this task turned out to be an elegant solution, and we were lucky to find him. Task Fees Laszlo Toth brought us to the idea of other, stronger hypotheses about the coverage of offset areas obtained by the intersection of the unit sphere with three-dimensional stripes-boards, not necessarily symmetrical relative to the center”.